Solutions Q40 - 44

# import all python add-ons etc that will be needed later on
%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
from sympy import *
init_printing()                      # allows printing of SymPy results in typeset maths format
plt.rcParams.update({'font.size': 14})  # set font size for plots

Q40 answer

(a) From the table of polarizer matrices, that for a polarizer at zero degrees is

\[\begin{split}\displaystyle \begin{bmatrix} 1 & 0 \\ 0 & 0 \end{bmatrix}\end{split}\]

The multiplication to produce the output beam is

\[\begin{split}\displaystyle \begin{bmatrix} 1 & 0 \\ 0 & 0 \end{bmatrix}\begin{bmatrix} V \\ H \end{bmatrix}=\begin{bmatrix} V \\ 0 &\end{bmatrix}\end{split}\]

which shows that the polariser selects just the vertical polarized light. The intensity is

\[\begin{split}\displaystyle \begin{bmatrix} V & 0 &\end{bmatrix}\begin{bmatrix} V \\ 0 &\end{bmatrix}=V^2\end{split}\]

so that the reflected light is the total less that transmitted, i.e.

\[\begin{split}\displaystyle \begin{bmatrix} V & H &\end{bmatrix}\begin{bmatrix} V \\ H &\end{bmatrix}-H^2=V^2\end{split}\]

which is not too surprising, and conforms to our own intuition.

(b) At \(45^\text{o}\) or \(\pi\)/4 radians, the matrix is

\[\begin{split}\displaystyle \begin{bmatrix} \cos^2(\pi/4) & \sin(\pi/4)\cos(\pi/4)\\ \sin(\pi/4)\cos(\pi/4) & \sin^2(\pi/4)\end{bmatrix}=\begin{bmatrix}1/2 & 1/2 \\1/2 & 1/2 \end{bmatrix}\end{split}\]

therefore

\[\begin{split}\displaystyle \begin{bmatrix}1/2 & 1/2 \\1/2 & 1/2 \end{bmatrix}\begin{bmatrix}V \\H \end{bmatrix}=\begin{bmatrix}(V+H)/2 \\(V+H)/2 \end{bmatrix}\end{split}\]

and because the componets are equal equal amounts of light are transmitted and reflected.

Q41 answer

With the wave-plate fast axis at some arbitrary angle \(\varphi\) and using the matrix from the table, the matrix equation is

\[\begin{split}\displaystyle \begin{bmatrix} 2\cos^2(\theta)-1 & 2\sin(\theta)\cos(\theta)\\ 2\sin(\theta)\cos(\theta) & 1-2\cos^2(\theta) \end{bmatrix}\begin{bmatrix} V \\0\end{bmatrix} =V\begin{bmatrix} 2\cos^2(\theta)-1 \\2\sin(\theta)\cos(\theta)\end{bmatrix}\end{split}\]

and the intensity

\[\begin{split}\displaystyle V^2\begin{bmatrix} 2\cos^2(\theta)-1 & 2\sin(\theta)\cos(\theta)\end{bmatrix}\begin{bmatrix} 2\cos^2(\theta)-1 \\2\sin(\theta)\cos(\theta)\end{bmatrix}\end{split}\]

expanding and simplifying produces an intensity of \(V^2\) as shown in the following Sympy calculation

theta, V = symbols('theta, V')   # notice way of writing a row and a column matrix
Int = V**2 * Matrix([ [ 2*cos(theta)**2 -1, 2*sin(theta)*cos(theta)]  ] )\
           * Matrix([ [2*cos(theta)**2-1], [2*sin(theta)*cos(theta)]  ] )
Int

\[\displaystyle \left[\begin{matrix}V^{2} \left(2 \cos^{2}{\left(\theta \right)} - 1\right)^{2} + 4 V^{2} \sin^{2}{\left(\theta \right)} \cos^{2}{\left(\theta \right)}\end{matrix}\right]\]

simplify(Int)

\[\displaystyle \left[\begin{matrix}V^{2}\end{matrix}\right]\]

The tangent of the rotation angle \(\psi\) produced by the wave-plate is the horizontal divided by the vertical component of the vector;

\[\displaystyle \tan(\psi)=\frac{2\sin(\theta)\cos(\theta)}{2\cos^2(\theta)-1}\]

Using Sympy to simplify gives

simplify(2*sin(theta)*cos(theta)/(2*cos(theta)**2-1) )

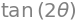
or \(\displaystyle \tan(\psi)=\tan(2\theta)\) or \( \psi=2\theta\) thus the rotation angle is then twice that rotated by the fast axis of the wave plate.

Q42 answer

(a) The matrix equation for the quarter-wave plate with its fast axis at \(0^\text{o}\) is \(\displaystyle \begin{bmatrix} 1 & 0\\0 & -i\end{bmatrix} \begin{bmatrix} V\\0\end{bmatrix}=\begin{bmatrix} V\\0\end{bmatrix}\) an has no effect on the beam. The transmitted intensity remains at \(V^2\).

(b) At \( \theta= 45^\text{o}\, \Delta=\pi/2\) and \(e^{-i\Delta}=-i\) the related equation is

\[\begin{split}\displaystyle \begin{bmatrix} \cos^2(\theta)-i\sin^2(\theta) & \sin(\theta)\cos(\theta)(1+i)\\ \sin(\theta)\cos(\theta)(1+i) & -i\cos^2(\theta)+\sin^2(\theta) \end{bmatrix} =\frac{1}{2} \begin{bmatrix} 1-i & 1+i\\1+i & 1-i\end{bmatrix}\end{split}\]

and the matrix equation

\[\begin{split}\displaystyle \frac{1}{2}\begin{bmatrix} 1-i & 1+i\\1+i & 1-i\end{bmatrix}\begin{bmatrix} V & \\ 0\end{bmatrix}=\frac{V}{2}\begin{bmatrix} 1-i \\1+i \end{bmatrix}\end{split}\]

therefore, the quarter wave plate at \(45^\text{o}\) produces elliptically polarized light, whose total intensity is calculated as the Hermitian dot product which means transposing the column vector to make a row, then take the complex conjugate. The result is

\[\begin{split}\displaystyle \frac{V^2}{4}\begin{bmatrix} 1+i & 1-i \end{bmatrix}\begin{bmatrix} 1-i \\1+i \end{bmatrix}=\frac{V^2}{4}(2+2) =V^2\end{split}\]

and no intensity is lost. Notice again that we make the complex conjugate when forming the row vector.

(c) In the general case the matrix equation is

\[\begin{split}\displaystyle \begin{bmatrix} \cos^2(\theta)-i\sin^2(\theta) & \sin(\theta)\cos(\theta)(1+i)\\ \sin(\theta)\cos(\theta)(1+i) & -i\cos^2(\theta)+\sin^2(\theta) \end{bmatrix}\begin{bmatrix} V\\0\end{bmatrix}=V\begin{bmatrix}\cos^2(\theta)-i\sin^2(\theta)\\(1+i)\cos(\theta)\sin(\theta)\end{bmatrix}\end{split}\]

and the intensity

\[\begin{split}\displaystyle V\begin{bmatrix}\cos^2(\theta)+i\sin^2(\theta)&(1-i)\cos(\theta)\sin(\theta)\end{bmatrix}V\begin{bmatrix}\cos^2(\theta)-i\sin^2(\theta)\\(1+i)\cos(\theta)\sin(\theta)\end{bmatrix}=V^2(\cos^2(\theta)+\sin^2(\theta))^2=V^2\end{split}\]

proving that any ideal wave-plate does not alter the intensity of a beam passing through it. This calculation clearly ignores any reflection at the surfaces, due to changes in the refractive index between the wave-plate and air.

Q43 answer

The experimental scheme is

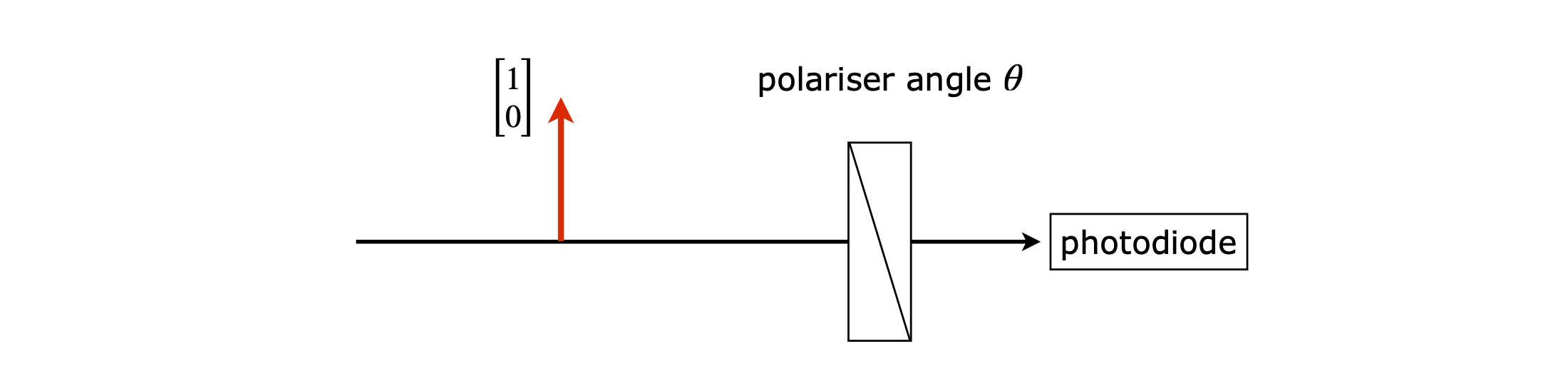
Figure 86. Experimental set-up.

---

The matrices are

\[\begin{split}\displaystyle \begin{bmatrix}E_V\\E_H \end{bmatrix}=\begin{bmatrix} \cos^2(\theta) & \sin(\theta)\cos(\theta)\\ \sin(\theta)\cos(\theta) & \sin^2(\theta) \end{bmatrix}\ \begin{bmatrix}1\\0 \end{bmatrix} \end{split}\]

where the output electric field amplitudes are \(E_V\) and \(E_H\) after going through the polarizer. Multiplying produces

\[\begin{split}\displaystyle \begin{bmatrix}E_V\\E_H \end{bmatrix}=\begin{bmatrix} \cos^2(\theta)\\ \sin(\theta)\cos(\theta) & \end{bmatrix}\ \end{split}\]

The transmitted intensity is then the dot product of this column with itself

\[\begin{split}\displaystyle I=\begin{bmatrix} \cos^2(\theta) & \sin(\theta)\cos(\theta) & \end{bmatrix}\begin{bmatrix} \cos^2(\theta)\\ \sin(\theta)\cos(\theta) & \end{bmatrix}=\cos^2(\theta)\end{split}\]

which shows that the transmitted intensity varies as \(\cos^2(\theta)\) and is a maximum when the polarizer is at \(0^\theta{o}\); that is when the polarization direction of the laser’s electric field and that of the polarizer are aligned. The transmitted intensity is zero when the laser polarization and polarizer direction are perpendicular (\(90^\text{o}\)) to one another. This is a very useful way of attenuating a laser’s intensity.

(b) The output Maxwell column

\[\begin{split}\displaystyle \begin{bmatrix}E_V\\E_H \end{bmatrix}=\begin{bmatrix} \cos^2(\theta)\\ \sin(\theta)\cos(\theta) & \end{bmatrix}\end{split}\]

is always real, so the light is linearly polarized and the angular direction of the polarization \(\psi\) from the vertical, is given by the angle of the polarizer \(\theta\) and is calculated using \(\tan(\psi) = \sin(\theta)/\cos(\theta)\) or \(\psi=\theta\). As the initial light is vertically polarized, no light is to be observed when the polarizer is at \(90^\text{o}\), but some is still observed at \(\lt 90^\text{o}\), according to the \(\cos^2(\theta)\) distribution.

Q44 answer

(a) We use particular matrices first and then use general ones in a second calculation.

theta = symbols('theta')
# define half wave plate HWP
HWP = Matrix([[2*cos(theta)**2-1,2*cos(theta)*sin(theta)],[2*cos(theta)*sin(theta),1-2*cos(theta)**2]])
HWP

\[\begin{split}\displaystyle \left[\begin{matrix}2 \cos^{2}{\left(\theta \right)} - 1 & 2 \sin{\left(\theta \right)} \cos{\left(\theta \right)}\\2 \sin{\left(\theta \right)} \cos{\left(\theta \right)} & 1 - 2 \cos^{2}{\left(\theta \right)}\end{matrix}\right]\end{split}\]

pol0 = Matrix([[1,0],[0,0]])  # polariser zero deg
pol90= Matrix([[0,0],[0,1]])  # polariser 90 deg
M = Matrix([[1],[0]])  

ans = pol90 * HWP * pol0 *M
ans

\[\begin{split}\displaystyle \left[\begin{matrix}0\\2 \sin{\left(\theta \right)} \cos{\left(\theta \right)}\end{matrix}\right]\end{split}\]

Intensity=ans.transpose()*ans
Intensity

\[\displaystyle \left[\begin{matrix}4 \sin^{2}{\left(\theta \right)} \cos^{2}{\left(\theta \right)}\end{matrix}\right]\]

solve(diff(Intensity,theta) ,theta )    # find maxima and minima.

The plot shows the maximum and minimum values clearly

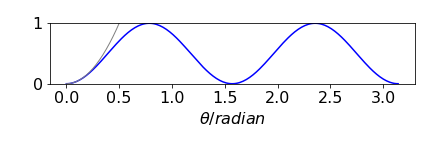
Figure 87. Variation of transmitted intensity with half-wave plate’s angle in radians. The gray line shows the limit at small angle, see part (c).

---

(b) The maximum is found at \(\pm 45^\text{o}\) to the vertical; minima between these positions at zero and \(90^\text{o}\) etc.

(c) At small angles where \(\theta <0.1\) radian, the intensity can be expanded as a series; (see Chapter 5)

\[\displaystyle I= 4\cos^2(\theta)\sin^2(\theta)\approx 4\left(1-\frac{\theta^2}{2!}+\frac{\theta^4}{4!}\cdots\right)^2 \left(\theta-\frac{\theta^3}{3!}+\frac{\theta^5}{5!}\cdots\right)^2\]

Because \(\theta \lt \theta^2\) and also for higher powers, on multiplying out gives all squared and higher terms are unimportant thus, \(I\approx 4\theta^2\) which may be confirmed by plotting this result. The transmitted intensity is proportional to the square of the angle when this is small.

(d) Now make the calculation general for any polarizer and wave-plate angles using Sympy.

theta, alpha, beta, delta = symbols('theta, alpha, beta, delta', real=True)

# theta is wave plate angle, beta and alpha polariser angles, delta phase for waveplate 

beta  = pi/2 
alpha = 0
delta = pi

Wave_plate = Matrix([[cos(theta)**2+sin(theta)**2*exp(-1J*delta), cos(theta)*sin(theta)*(1-exp(-1J*delta))]\
                   ,[cos(theta)*sin(theta)*(1-exp(-1J*delta)), sin(theta)**2+cos(theta)**2*exp(-1J*delta)]])
Wave_plate

\[\begin{split}\displaystyle \left[\begin{matrix}e^{- 1.0 i \pi} \sin^{2}{\left(\theta \right)} + \cos^{2}{\left(\theta \right)} & \left(1 - e^{- 1.0 i \pi}\right) \sin{\left(\theta \right)} \cos{\left(\theta \right)}\\\left(1 - e^{- 1.0 i \pi}\right) \sin{\left(\theta \right)} \cos{\left(\theta \right)} & \sin^{2}{\left(\theta \right)} + e^{- 1.0 i \pi} \cos^{2}{\left(\theta \right)}\end{matrix}\right]\end{split}\]

pola = Matrix([[cos(alpha)**2,cos(alpha)*sin(alpha)],[cos(alpha)*sin(alpha),sin(alpha)**2]])

polb = Matrix([[cos(beta)**2,  cos(beta)*sin(beta) ],[cos(beta)*sin(beta),   sin(beta)**2]])

M = Matrix([[1],[0]])  # vert pol input beam

out = polb*Wave_plate*pola*M   
simplify(out)

\[\begin{split}\displaystyle \left[\begin{matrix}0\\\sin{\left(2 \theta \right)}\end{matrix}\right]\end{split}\]

Intensity=simplify((out.conjugate() ).transpose()*out )
Intensity 

\[\displaystyle \left[\begin{matrix}\frac{1}{2} - \frac{\cos{\left(4 \theta \right)}}{2}\end{matrix}\right]\]