Questions 15-30

All these questions,except the last, are of a mathematical nature.

Q15

Evaluate

\(\displaystyle \begin{array}{llll}\\ \text{(a) } I=\int\cos^3(x)dx & \text{(b) }\displaystyle I=\int \frac{3x}{(5+3x)^4}dx & \text{(c) } \displaystyle I=\int \frac{e^\sqrt{x}}{\sqrt{x}}dx \\ \text{(d) }\int \cot(ax)dx & \text{(e) }\displaystyle I=\int\frac{x^2}{8+x^3}dx &\text{(f) }\displaystyle \int \frac{e^{ax}}{1-e^{ax}}\\ \end{array}\)

Q16

Find \(\displaystyle I=\int \frac{1}{\sqrt{b^2-x^2}}dx\).

Strategy: You might well decide at this point to try using Sympy as this integration is looking quite complicated and the substitution to use is not obvious. Evaluation can sometimes be successful by starting with

\[\displaystyle b^2\cos^2(u) + b^2\sin^2(u) = b^2 \quad\text{ or }\quad b\cos(u) =\sqrt{ b^2 - b^2\sin^2(u)}\]

Make the substitution \(x = b \sin(u)\) and its differential \(dx = b \cos(u)du\).

Q17

(a) Integrate \(\displaystyle I=xe^{-x^2}dx\) and

(b) Evaluate and plot the function from \(x = -3 \to 3\) and the result of the integration from \(0 \to x\).

Q18

Integrate \(\displaystyle I=\int\frac{x-2}{x\sqrt{x+3}}dx\) by hand and using Sympy.

Q19

Evaluate \(\displaystyle I=\int_{-1}^2\frac{x^2}{16+x^2}dx\)

Q20

Determine by parts \(I = \int\sin^{-1}(ax)dx\).

Q21

The integral \(\displaystyle Ei(x) = -\int_{-x}^\infty \frac{e^{-t}}{t}dt\)

is called the exponential integral and cannot be evaluated explicitly but only numerically. It can occur in the calculation of molecular orbitals.

(a) Show that \(\displaystyle Ei(-x) = \int_x^\infty \frac{e^{-t}}{t}dt=\int_{-\infty}^x \frac{e^{t}}{t}dt\).

(b) Expand \(Ei(x)\) by parts and form a series expansion of the integral.

Q22

(a) Integrate \(I=\int xe^{ax}dx\)

(b) Sometimes integrals can be written in terms of others. Suppose that

\[\displaystyle I_0=\int e^{ax}dx, \;I_1=\int xe^{ax}dx,\; I_2=\int x^2e^{ax}dx \]

By induction find \(I_n=\int x^ne^{ax}dx\) where \(n\) is a positive integer.

Strategy: Calculate by parts \(I_2\) and \( I_3\). ‘By induction’ effectively means look for a pattern in the answers and find the \(n^\text{th}\) term.

Q23

integrate by parts

(a) \(\displaystyle I_1 = \int_0^\infty xe^{-ax^2} dx\)

by choosing \(v = e^{-ax^2}\) and \(u = 1\). This is an alternative method to that in Q17.

(b) \(\displaystyle I = \int_0^\infty n^n e^{-ax^2} dx\)

to find a recurrence relationship between \(I_n\) and \(I_{n+2}\).

Strategy: Look at the general form of the ‘by parts’ integral, work out what \(dv\) is and rewrite the integral.

Q24

Integrate \(\displaystyle I=\int \frac{\cos(\ln(|x|)}{x}dx\).

Strategy: Find \(d\ln(x)\) and then make a substitution.

Q25

Find \(\int \sec^2(\sqrt{x})dx\).

Q26

Integrate by parts

(a) \(I = \int \cosh(x)\sinh(x)dx\),

(b) \(\int x\cos(x)dx\).

Q27

Integrate \(\displaystyle \int \frac{dx}{\sin(ax)}\). Is your answer the same as given by SymPy?

Strategy: Convert the sine to its exponential form then try a substitution.

Q28

(a) find \(\displaystyle \int_{-\pi}^{\pi}dx\),

(b) Show that \(\displaystyle \int_{-\pi}^\pi e^{imx}e^{-inx}=2\pi\delta_{n,m}\)

where \(m\) and \(n\) are integers. If \(m = n\) then the delta function \(\delta_{n,m} = 1\), otherwise it is zero.

Q29

Occasionally it is possible to evaluate some definite integrals by engaging in subterfuge, changing the integral and differentiating first.

Evaluate the Sine Integral

\[\displaystyle Si(w)=\int_0^w\frac{\sin(x)}{x}dx\]

but with an upper limit of infinity, i.e.

\[\displaystyle I =\int_0^\infty \frac{\sin(x)}{x}dx\]

by first multiplying by \(e^{-\beta x}\) to produce

\[\displaystyle I =\int_0^\infty e^{-\beta x}\frac{\sin(x)}{x}dx\]

and then differentiating w.r.t. \(\beta\). Next integrate twice over, first with respect to \(x\) and then with respect to \(\beta\). Use the limits zero and infinity for the first integration. Finally calculate what happens when \(\beta = 0\), thus making the exponential term unity and so returning the original integral.

The other limit is infinity because this makes \(I_\beta = 0\). You will find that the initial differentiation removes the denominator, making the integral simpler. It is an integral met before and one that can be performed by parts; see Section 5.

Q30 Soap films

The equation describing the shape of the soap film described in Q 82 may be derived by considering the surface tension \(T\) of the film. Every point on a vertical circle around the film has an equal horizontal surface tension, which is equal to a constant \(c\). Therefore, \(2\pi yT \cos(\theta) = c\). By calculating the cosine for small changes of \(x\) and \(y\) in the limit of \(dy\) and \(dx\), find an equation for \(dy/dx\). Separate this into integrals in \(y\) and \(x\) and integrate both sides to find the equation for \(y\), the film,s radius. Finally convert the equation into a hyperbolic trig form.

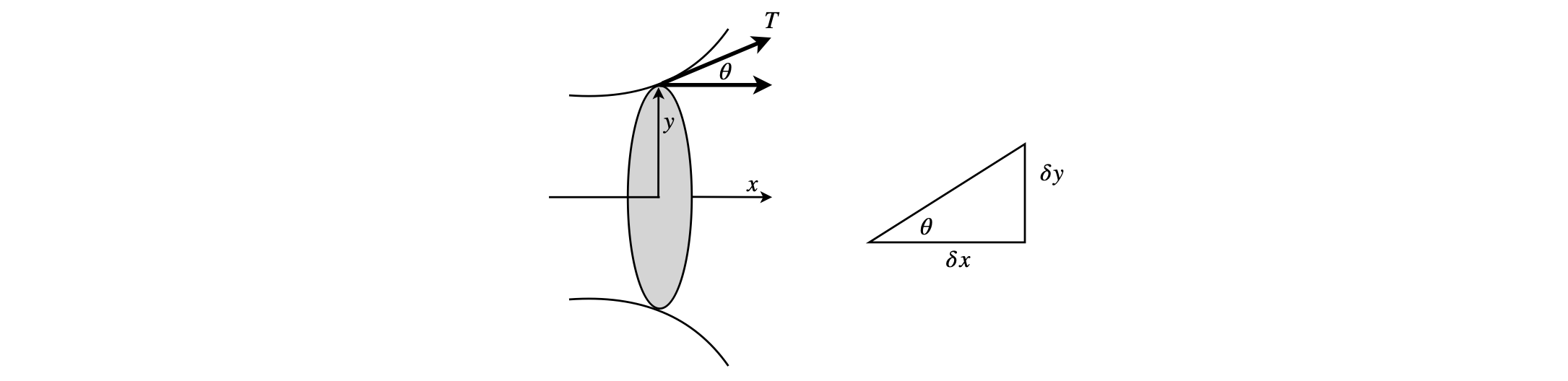
Figure 8. Geometry for Q30.