Questions 59 - 61

Q59 Cross product

The differential of a cross product is \(\displaystyle \frac{d}{dt}(\vec A \times \vec B)=\vec A \times \frac{d\vec B}{dt}+\frac{d\vec A}{dt}\times \vec B\). Calculate \(d\vec L/dt\) if \(\displaystyle \vec L=m\vec v \times \frac{d\vec r}{dt}\).

Q60 Centripetal acceleration

A particle with orbital motion has a centripetal acceleration of \(\vec a = \vec \omega\times (\vec \omega \times \vec r)\), where \(\vec \omega\) is angular velocity and \(\vec r\) a positional vector. Find \(|\vec a|\) if the motion is in a circle where \(\vec r\) and \(\vec \omega\) are perpendicular.

Q61 Rotating disc

Derive the equation for the linear velocity of a disc, and by inference any rigid body, using the \((i, j, k)\) basis set of vectors. Although these are fixed in space they may be used by allowing the amplitude of the vector’s components to change with rate \(\alpha\) which is also the magnitude of the angular velocity \(\vec \omega\),

\[\displaystyle \vec r(t) = \vec r\cos(\alpha t)\;\boldsymbol i + \vec r\sin(\alpha t)\;\boldsymbol j\]

Calculate the cross product \(\vec \omega \times\vec r\) and the position vector \(\vec r\). Next, differentiate \(\vec r\) to obtain the linear velocity \(\vec \upsilon\) and equate the two equations. Figure 55 shows the definition of vectors. Let \(r\) be the magnitude of vector \(\vec r\).

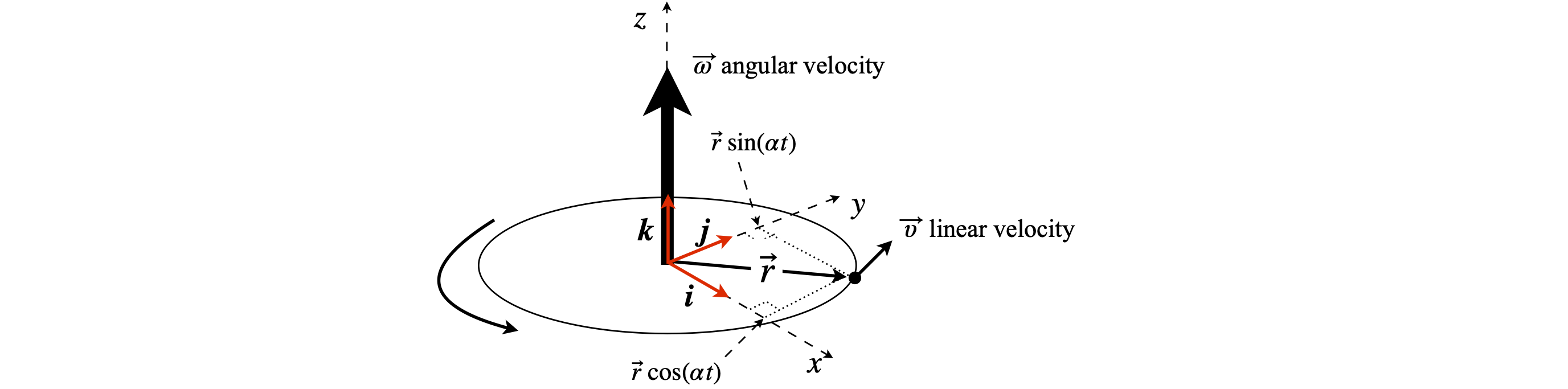
Figure 55 Angular velocity \(\vec \omega\), linear velocity \(\vec \upsilon\) of a disc of radius \(r\) with radius vector \(\vec r\).