Questions 17 - 20
Contents
Questions 17 - 20#
Q17 SIR equations#
Calculate Fig. 17, and confirm the numbers in the calculation.
Strategy: Use the code and parameters given in the text. Vary the rate constants to get an idea of the sensitivity of the fit to these values.
Q18 SIR equations#
Use Python’s ‘solve’ routine routine to integrate the SIR equations, or use your own Euler routine, using the data in Fig. 17, but automate the fitting by using a very simple, but inefficient, grid search to vary \(k_2\) and \(k_1\) with \(10\) values each, incrementing each value and so find the optimum values. Use two do loops to do this, setting back to the initial values one of the rate constants after the inner loop is completed but allowing the other to vary. Estimate the ‘goodness’ of each fit by calculating the residual which is the sum of the square of the difference between each of the calculated values and the corresponding data point; \(\sum_i (calculated_{indx[i]} - data_i )^2\). The number of calculated and the number of data points differ greatly so to find the residual the calculated data has to be samples at exactly the time set by the data point, this is the meaning of the \(indx[i]\). Make a contour plot to determine the range where the best parameters fitting the data can be found.
The square of the difference is taken in the residual because some differences may be negative. As smaller values of the residual are found, narrow the search area to ‘home in’ on the best estimates. The grid search is a slow but effective way of searching.
Using the SIR model, confirm that \(k_2\) is in the range \(0.001 \to 0.004\,\mathrm{ day^{-1}}\) and \(k_1\) is in range \(0.2 \to 0.6\,\mathrm{ day^{-1}}\).
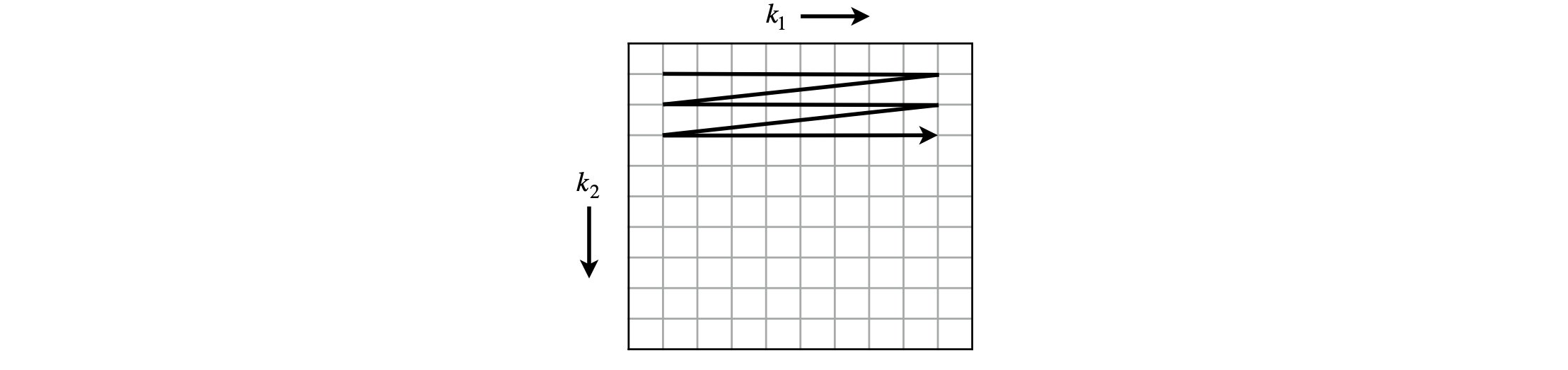
Figure 18. grid search.
Q19 Recalculate eqn. 32#
Recalculate equation 32 (section 5) but with initial values \(x_0 = 2,\; y_0 = 1\), and \(t_0 = 0\) over the range \(0 \to 10\) and then with the modified Euler method. The result is unexpected, increase \(N\) and the precision of the calculation. Try to explain why the calculation fails. Repeat with Python’s built-in routine.
Q20 SIR#
The data set ‘UK-covid-deaths.txt’ contains the cumulative deaths where the last number on the list is \(2\) March \(2020\). The data can be found at the end of the appendix ‘Some basic Python instructions with a few examples’ at the very end of this book. Note that the data is in reverse order so will need to be reversed before using.
(a) Estimate the data for the first \(180\) days of the pandemic using the SIR model. The kinetic scheme will need to be modified to include deaths by assuming that some patients in the infected group \(I\) die with rate constant \(k_d\), assume that \( k_d=9\cdot 10^{-4}\) and that two million people are initially susceptible.
(b) Plot your fit and that of the number of daily deaths, obtained by numerically differentiating the data and calculated data as \(\Delta\)(number)/ \(\Delta\)(time). The \(\Delta\)(time) will be one day for the data but the time increment in your calculation for the calculated data. As the number of persons is very large and the \(R_0\) for Covid is between approximately \(3\) and \(6\), by using the equations in the text, \(k_2\) must be very small, \(\approx 10^{-7}\).
Strategy To add the equation for death rate follow how the other species are treated in the Euler algorithm. To fit the data with rate constants \(k_1\) and \(k_2\) you will have to estimate values by trial and error to begin with based on initial guesses using equations in the text. The grid search method can then be used; see question Q18. To appreciate what is at stake here imagine that public policy, such as to enter/extend lockdown or not or deliver vaccinations more quickly etc., depends on your accurate modelling of this data.


