Questions 7 - 10#

Q7 Singlet excited state decay#

A singlet excited state decays to a triplet state by intersystem crossing with a rate constant, \(k_{isc} = 2 \cdot 10^8\,\mathrm{ s^{-1}}\), as well as fluorescing to the ground state with rate constant \(k_f = 1 \cdot 10^7\,\mathrm{ s^{-1}}\).

(a) What is the fluorescence lifetime and the fluorescence yield?

(b) Assume that the triplet state has a 20 ns decay time, \(k_T = 1/(20\) ns). Calculate the fluorescence decay as well as the rise and fall in the triplet population for at least \(100\) ns, using a Monte Carlo method.

Strategy: The yield and lifetime are very easy to calculate. The fluorescence lifetime is the reciprocal of the sum of the rate constants depleting the excited singlet \(\tau = 1/(k_f + k_{isc})\). The fluorescence yield is the fraction of molecules that fluoresce compared to the total number of excited states, which is the same as the rate constant for fluorescence divided by the total of all rate constants causing the state to decay, \(\varphi = k_f /(k_f + k_{isc}) = k_f\tau\) (see Turro 1978). All yields must be between 0 and 1. The calculation is similar to that in the examples, but now two reactions are present, the singlet and triplet. The rate equations are

\[\displaystyle \mathrm{S}\overset{ k_{isc}} \longrightarrow T, \qquad \mathrm{S}\overset{ k_f}\longrightarrow \mathrm{S_0},\qquad \mathrm{T}\overset{ k_T}\longrightarrow \mathrm{S_0}\]

where S is the excited state, T the triplet and S\(_0\) the ground state. The populations are calculated as in the Gillespie Algorithm for excited states modified for the decay of the triplet. This means that three checks need to be made as there are three possible transitions, excited singlet to triplet, excited singlet to ground state, and triplet to ground state. Work out the sum \(a_0\) then the fraction of this that corresponds to each type of transition and compare this to a random guess as to which one will be chosen.

Q8 Excited state blocking#

We have assumed in previous calculations that the population of the final state does not affect the transition from other states, but, in fact, the rate of a transition is proportional to the difference in population between energy levels. Two common situations arise where the final state population can affect the transition from an upper level; one is a three or four level laser and the other is the phenomenon of band filling in semiconductors, where, because of the Pauli principle, only two electrons can fill any electronic energy level. A generic diagram is shown in Figure 8. It is assumed that state \(T\) is full when it receives half the total population.

Calculate the decay of state A if \(k_f = 1/(100\mathrm{ ns})\) and \(k_{isc} = 1/(30\, \mathrm{ns})\). Assume that the probability of going into state \(T\) is reduced in proportion to the fraction of the total number already in that state.

Strategy: The excited state lifetime is \(1/(k_f + k_{isc})\), but \(k_{isc}\) is a function of the population in level \(T\) so the lifetime changes as time progresses. This can be accommodated by making a function

\[\displaystyle k_2(n) = \left(1 - \frac{2n_T}{n}\right)k_{isc}\]

where \(n_T\) is the number in level \(T\) at any state of the calculation. At the start, \(n_T = 0\) and therefore \(k_2(n) = k_{isc}\), and at the end \(n_T = n/2\), and \(k_2(n) = 0\). As time progresses, proportionately more and more population enters state G because the value of \(k_2(n)\) becomes smaller. Start by modifying the code in the solution to Q7).

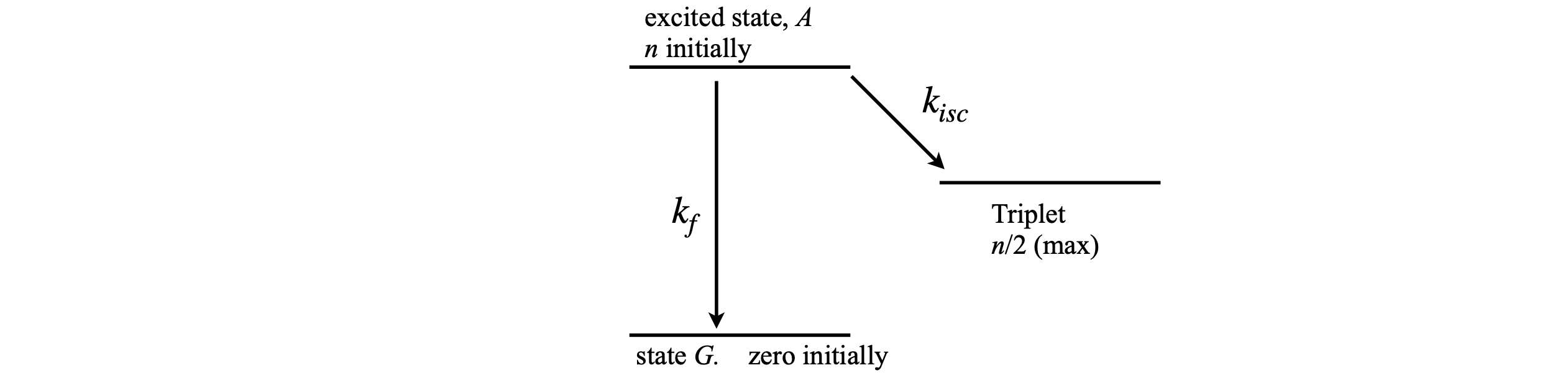
Drawing

figure 8. A scheme where population difference becomes important.

Q9 SIR model of disease#

The S-I-R scheme describes the way an infection is passed among individuals and is described in detail in Chapter 11.7. The scheme is

\[\displaystyle S+I \overset{k_{SI}}\longrightarrow 2I, \qquad I\overset{k_{IR}}\longrightarrow R \]

and this will be solved using the Gillespie Monte Carlo method. \(S\) represents the number of susceptible persons, \(I\) the number infected, and \(R\) those removed, i.e. those who have had the infection, and are otherwise immune. The rate equations are

\[\displaystyle dS/dt = -k_2SI, \qquad dI/dt = +k_2SI - k_1I, \qquad dR/dt = +k_1I\]

The data is taken from Chapter 11.7.5 and relates specifically to an infection in a boys’ school; \(k_{SI} \equiv k_1 = 2.18 \cdot 10^{-3}, \; k_{IR} \equiv k_2 = 0.452\) hours. The initial S population \(S_0\), is 762 and one person is initially infected, \(I_0 = 1\). The equations can of course be solved without knowing the underlying science; the equations could just as easily be (autocatalytic) chemical species where R, once formed, does not react. It will be necessary to repeat the calculation several times, to obtain good averaged data.

Strategy: The method to use is similar to that outlined in the examples. The question gives all the information needed except the number of bins to calculate the data over; 100 should be sufficient which is one data point every 5 hours. To improve the calculation, several runs may have to be calculated and averaged.

Q10 Predator - prey model#

The Lotka - Volterra, predator - prey scheme is

\[\displaystyle Y\overset{k_1}\longrightarrow Y+Y,\qquad Y+X \overset{k_2}\longrightarrow X+X, \qquad X\overset{k_3}\longrightarrow Q \tag{12}\]

where Y is the prey and X the predator. The rate equations are

\[\displaystyle \frac{dY}{dt} = k_1Y − k_2YX, \qquad \frac{dX}{dt} = k_2YX − k_3X \]

These equations are described in more detail in Chapter 11.8.1 where they are solved numerically.

Solve these equations by using the Gillespie Monte Carlo method to calculate the time profile of species Y and X over \(200\) time units with initial values, \(Y_0 = 400,\; X_0 = 100,\; k_1 = 0.5,\; k_2 = 0.001, \;k_3 = 0.5\). Use \(1000\) time bins. Comment on the results.

Strategy: Use the model as in the text, making sure that \(a_0\) is calculated correctly. Do not forget that there are three reactions, so three choices have to be made as to which reaction is occurring at any time. If you also plot the phase plane this is, not surprisingly, very random compared to a direct numerical solution.