Questions 45 - 48#

Q45 Particle in sloping box#

Repeat the particle in box example calculation and with a perturbing potential of the form \(V = b(x-L/2)^2\) making it zero in the centre of the box. The constant is \(b = 1/4\). Use python, based on the code in the example or otherwise, to calculate some of the energy corrections \(E(1),\;E(2)\) etc.

Q46 Diatomic molecule in electric filed#

A heteronuclear diatomic molecule, which can be adequately described as a harmonic oscillator, is placed in an electric field aligned with the molecule’s long axis and so experiences an additional and linear potential of magnitude \(ax\). Calculate the change in the energy levels and the resulting spectrum. The harmonic oscillator has vibrational frequency \(\omega\) and reduced mass \(\mu\) and orthonormal wavefunctions,

\[\displaystyle \psi(x,n) = \frac{1}{\sqrt{2^n n!}}\left(\frac{\alpha}{\pi}\right)^{1/4}H_n(x\sqrt{\alpha}) e^{-ax^2/2}\]

where \(\displaystyle \alpha = \sqrt{k\mu/\hbar}\) and \(\displaystyle H_n(x\sqrt{\alpha})\) is a Hermite polynomial. You should look these up and either use a recursion formula to calculate values or use the formulae directly is you use only a few.

Strategy: Use the perturbation method to calculate the change in energy. In each case use the harmonic oscillator wavefunctions. The Hamiltonian is \(H = H^0 + ax\) where \(H^0\) solves the normal harmonic oscillator with energy \(\displaystyle E_n = \hbar \omega (n + 1/2)\).

Q47 Perturbed harmonic oscillator#

Suppose that a harmonic potential is modified by a perturbing cubic term of magnitude \(bx^3\), the oscillator now becomes anharmonic. Calculate the energy levels and spectrum.

Q48 Particle on a ring with potential#

The particle on a ring can approximate the energy levels of a cyclic polyene. The potential energy is zero and the Schroedinger equation

\[\displaystyle -\frac{\hbar^2}{2\mu}\frac{d^2\psi}{d\varphi^2}=E\psi\]

where the angle \(\varphi\) has values from \(-\pi \cdots \pi\) radians. The wavefunction is

\[\displaystyle \psi_n= e^{in\varphi}/\sqrt{2\pi}\]

and the quantum numbers are \(n = 0, \pm 1, \pm 2, \cdots\)

(a) Calculate the unperturbed energies \(E_n\).

(b) Calculate the perturbed energy of the lowest level (\(n = 0\)) to second order, when the potential has the value \(V\) from \(-a\pi \cdots a\pi\) where \(a\) is a fraction \(\lt 1\). If we were to suppose that our ring was pyridine then the nitrogen would have a different potential to that of the carbons. Call this value \(V\), and then \(a\) could be 1/6. Find the energy if \(V = 0.1E_1\). The figure shows a particle on a ring with a small region of perturbation.

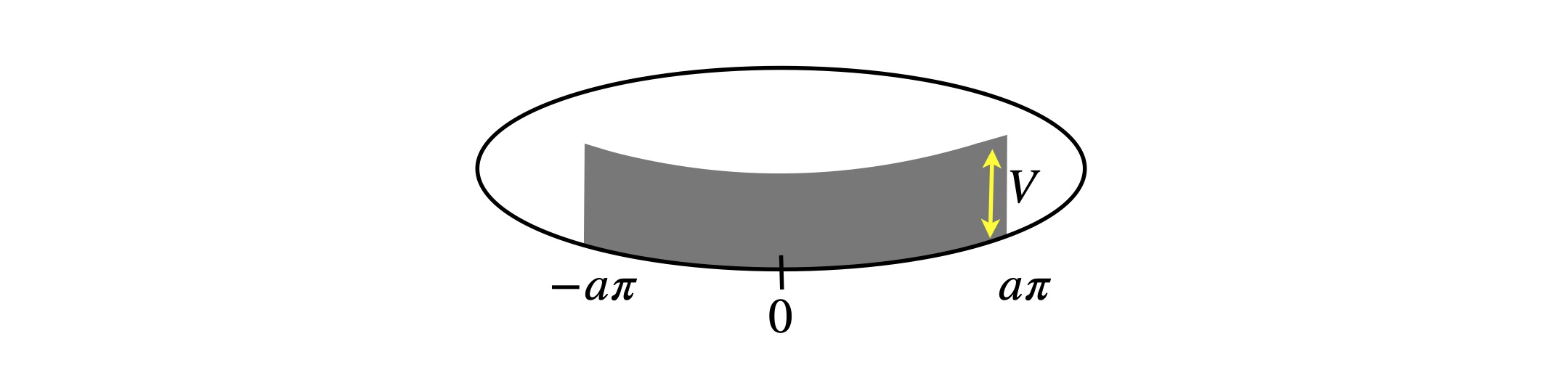
Drawing

Figure 14. Particle on a ring with a small region of perturbation