Solutions Q 1-11

# import all python add-ons etc that will be needed later on
%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
from sympy import *
init_printing()            # allows printing of SymPy results in typeset maths format
plt.rcParams.update({'font.size': 14})  # set font size for plots

Q1 answer

Rearranging the equation produces \(V=1000/p \) and then a new function for the increased volume is produced by adding the small quantities \(\delta V\) and \(\delta p\),

\[\displaystyle (V + \delta V) = \frac{1000}{ p + \delta p}\]

and the change in volume with pressure is therefore

\[\displaystyle \delta V=(V+\delta V)-V-\frac{1000}{p+\delta p}-\frac{1000}{p}=\frac{1000\delta p}{p(p+\delta p)}\]

The change in volume when the pressure changes from \(1 \to 1.1\) bar is \(-1000 \cdot 0.1/1.1 = -90.91\,\mathrm{ m^3}\) and is negative because the pressure has increased.

Q2 answer

(a) The new frequency is lower when \(μ\) is increased, because \(\nu\) and \(\mu\) are in a reciprocal relationship. Therefore

\[\displaystyle \nu- \delta \nu=\frac{1}{2\pi}\sqrt{\frac{k}{\mu+\delta\mu}}\]

and the change is

\[\displaystyle \delta \nu=-\frac{1}{2\pi}\sqrt{\frac{k}{\mu+\delta\mu}}+\frac{1}{2\pi}\sqrt{\frac{k}{\mu}}\]

and the relative change

\[\displaystyle \frac{\delta\nu}{\nu}=-\sqrt{\frac{\mu}{\mu+\delta\mu}}+1\]

This is a very awkward expression to simplify because, by letting

\[\delta\mu \to 0,\,\displaystyle \frac{\delta\nu}{\nu}=-\sqrt{\frac{\mu}{\mu+\delta\mu}}+1 \to 0\]

This is incorrect because the square root terms are not taken to the limit properly. Rewriting the equation as

\[\displaystyle \frac{\delta\nu}{\nu} =-\sqrt{\frac{\mu}{\mu+\delta\mu}}+1=-\frac{1}{\sqrt{1+\delta\mu/\mu }}+1\]

enables the limit to be taken because \(\delta\mu/\mu \lt 1\). Series expansions are described in Chapter 5 but using the result given in the question

\[\displaystyle (1+x)^{-1/2} =1-x/2+3x^2/8-\cdots\]

therefore

\[\displaystyle \frac{\delta\nu}{\nu}=\frac{1}{2}\frac{\delta\mu}{\mu}\]

and you can justify halting the expansion at the first term because \(\delta\mu/\mu \lt 1\) and therefore \((\delta\mu/\mu)^2\) is even smaller.

(b) Using values in the question, the relative change \(\delta\nu/\nu = 0.01\) and before calculating the frequency this must be changed into s\(^{-1}\) from cm\(^{-1}\). The wavenumber or cm\(^{-1}\) is frequently used in spectroscopy because its numerical value is easier to remember and use than a frequency expressed in s\(^{-1}\). The conversion requires us to multiply by \(c\), the speed of light, hence \(5889.0\,\mathrm{ cm^{-1}} \equiv 2.997924 \cdot 10^{10}\,\mathrm{ cm\, s^{-1} \cdot 5889.0\, cm^{-1}} = 1.7655 \cdot 10^{14}\,\mathrm{ s^{-1}}\). The frequency change is \(58.89\,\mathrm{ cm^{-1}}\) or \(1.7655 \cdot 10^{12}\,\mathrm{ s^{-1}}\).

The problem could perhaps more usefully have been posed the opposite way round; by knowing that the resolution of a spectrometer is \(\nu \pm \delta \nu\) will it be possible to observe a line from two isotopic species whose mass differ by \(1\)%?

Q3 answer

The change in volume is \(\displaystyle V-V_0 =\delta V = V_0\beta \delta T \)

and so the change in length of the column of liquid is \(\displaystyle \delta L =\frac{V_0}{\pi r^2}\beta\delta T\)

for \(\delta T\) change in temperature. Substituting for the parameters produces

\[\displaystyle \frac{\delta L}{\delta T}=\frac{10^{-6}}{3.14(0.06\cdot 10^{-3})^2}\beta =88.4\beta\,\mathrm{ m \,K^{-1}}\]

With Hg this corresponds to a sensitivity of \(16\,\mathrm{ mm\, K^{-1}}\) and with ethanol \(95.5\,\mathrm{ mm\, K^{-1}}\). A fine capillary over a bulb of mercury is used in medical thermometers to make the readings very sensitive around body temperature. The capillary is so thin that violent shaking of the thermometer is necessary to overcome the capillary forces to return the mercury to its reservoir after use.

Q4 answer

\(\displaystyle \begin{array}{lll}\\ \hline (a)&(i) &dy/dx &= &12x^3 + \cos(x)\\ &(ii) &dy/dx &= &-40x{-5} + 10x\\ &(iii) &\displaystyle \frac{dy}{dx}&=&\displaystyle \frac{1}{x}-\frac{1}{ax^2}\\ &(iv) &dy/dx &= &ae^{ax} + 2x\\ \hline (b)& (i) &dy/da&=&0\\ &(ii) &dy/da&=&xe^{ax}\\ &(iii) &dy/da&=&x^2\\ \hline \end{array}\)

(c) Differentiating \(\sin(ax)\) five times gives the sequence

\(\displaystyle \begin{array}\\ dy/dx &= a \cos(ax)& d^2y/dx^2 &= -a^2 \sin(ax)&d^3y/dx^3&=-a^3\cos(ax)\\ d^4y/dx^4&=a^4\sin(ax)& d^5y/dx^5&=a^5\cos(ax)\end{array}\)

The identity \(\cos(ax) = \sin(ax + n\pi/2)\) is now needed and this changes the odd numbered results into sines, for example \(d^5y/dx^5 = a^5 \sin(ax + 5\pi/2)\). The result follows by inspection \(d^ny/dx^n = a^n \sin(ax + n\pi/2)\) with \(n \ge\) 1.

Q5

Using the rules for differentiating \(x^n\), start by differentiating once, twice, and so on to obtain

\[\displaystyle \frac{d}{dx}x^n=nx^{n-1},\quad \frac{d^2}{dx^n}x^n=n(n-1)x^{n-2},\quad \frac{d^3}{dx^3}x^n=n(n-1)(n-2)x^{n-3}\]

A pattern is becoming clear and can be generalized to the \(m\)^th differential without actually doing it;

\[\displaystyle \frac{d^m}{dx^m}x^n=n(n-1)(n-2)\cdots(n-m+1)x^{n-m}=\frac{n!}{(n-m)!}x^{n-m}\]

The product \(n(n - 1)(n - 2)\cdots(n - m + 1)\) looks a little like the factorial for \(n\), which can be written as

\[\displaystyle n! = n(n - 1)(n - 2)\cdots(n - m)(n - m + 1)(n - m + 2)\cdots 2\cdot 1\]

However, the ratio of factorials in the equation is found by trial and error and by testing with some real numbers if necessary. This approach is sometimes called ‘by inspection’ in textbooks. Making the \(n^{th}\) term by letting \(n = m\), produces \(x^{n - m} = 1\) and because \(0! = 1\) the result is \(\displaystyle \frac{d^n}{dx^n}x^n=n!\).

This type of approach is general in the sense that to find \(n\) terms an intermediate term \(m\) is chosen to be a general term and then \(m = n\) is made in the last step. The code using SymPy is given next.

x,y,n = symbols('x y n')    # define symbols to use 
ans = diff(x**n,x,x,x,x,x)  # differentiate 5 times   
factor(ans)

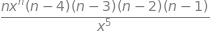
print(ans.subs(n,5),factorial(5) )  # substitute into ans and check answer is a factorial

120 120

Q6 answer

As \(\displaystyle \frac{dy}{dx}=-ae^{-ax}=-ay,\; \frac{d^2y}{dx^2}=a^2e^{-ax}=a^2y,\; \frac{d^3y}{dx^3}=-a^3y \)

by induction the \(n^{th}\) term is going to be \(\displaystyle \frac{d^ny}{dx^n}=(-1)^na^ny\),

where \((-1)^n\) makes the sign of the differential negative for odd \(n\) and positive for even \(n\); for example \((-1)^{(-1)} = 1\).

Q7 answer

(a) As \(pV=nRT\) for \(n\) moles of gas, then \(p=nRT/V\). Differentiating with respect to \(V\) produces

\[\displaystyle \frac{dp}{dV}=-\frac{nRT}{V^2}\]

where, by comparison with the equation in the question, the constant \(c = -nRT\).

(b) Rearranging the ideal gas equation to \(V=nRT/p\) leads to \(\displaystyle \frac{dV}{dp}=-\frac{nR}{p^2}\).

(c) By substitution \(\displaystyle \frac{dV}{dp}=-\frac{V^2}{nRT}\) then by comparison with (a) \(\displaystyle \frac{dV}{dp}=\left( \frac{dp}{dV}\right)^{-1}\).

This latter result is in fact quite general and \(\displaystyle \frac{dy}{dx}=\left( \frac{dx}{dy}\right)^{-1}\).

Q8 answer

Velocity is distance travelled per unit of time and therefore differentiating with respect to time produces the velocity at time \(t\), \(\displaystyle \frac{ds}{dt}\equiv v=u+at\).Differentiating again, produces \(d^2s/dt^2 = a\), so that \(a\) must be the acceleration as this is defined as distance/time².

Q9 answer

(a) The first two derivatives with \(t\) are

\[\displaystyle \frac{dE}{dt}=i\omega Ae^{i(\omega t-kx+\varphi)}=i\omega E\qquad \frac{d^2E}{dt^2}=i\omega \frac{dE}{dt}= (i\omega)^2E\]

and so it seems reasonable to conclude that by induction

\[\displaystyle \frac{d^nE}{dt^2}= (i\omega)^nE\]

(b) The related calculation for the distance is

\[\displaystyle \frac{dE}{dx}=-ik Ae^{i(\omega t-kx+\varphi)}=-ik E\]

and therefore \(\displaystyle \frac{d^nE}{dx^n}=(-ik)^n E\).

These results indicate that

\[E = Ae^{i(\omega t-kx+\varphi)}\]

is a general solution to the sets of differential equations

\[\displaystyle \frac{d^nE}{dx^n}=(-ik)^n E \qquad \frac{d^nE}{dt^n}=(i\omega)^n E\]

Q10 answer

(a) Starting with the first equation, simplifying, and using \(d\ln(c) = dc/c \) gives

\[\displaystyle D_F\frac{dc}{dx}=CD\frac{d\ln(c\gamma)}{dx}=cD\left[\frac{d\ln(c)}{dx}+\frac{d\ln(\gamma)}{dx} \right] =D\frac{dc}{dx}+cD\frac{d\ln(\gamma)}{dx}\]

Multiplying both sides by \(dx/dc\) and again using \(d \ln(c) = dc/c\) gives

\[\displaystyle D_F=D+cD\frac{d\ln(\gamma)}{dx}\frac{dx}{dc}=D+cD\frac{d\ln(\gamma)}{dc}=D\left[1+\frac{d\ln(\gamma)}{d\ln(c)}\right]\]

(b) The differential is

\[\displaystyle \frac{\ln(\gamma)}{d\ln(c)}=c\frac{d\ln(\gamma)}{dc}=-\frac{c}{2}\frac{Ac^{-1/2}}{(1+B\sqrt{c})}+\frac{c}{2}\frac{AB}{(1+B\sqrt{c})^2}=-\frac{A\sqrt{c}}{2(1+B\sqrt{c})^2}\]

Using SymPy confirms this result.

A,B,c,g = symbols(' A B c g')     # use g instead of gamma 
lngamma = -A*sqrt(c)/(1+B*sqrt(c))
ans = diff(lngamma,c)
simplify(ans*c)                   # don't forget to multiply by c after differentiating

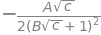
Q11 answer

Use equation(15) with \(v(x)\) = 0 and \(u(x)=a/x\) gives

\[\displaystyle \frac{d}{dx}\int_0^{a/x}\frac{x^2}{e^{-x}-1}dx =\left(\frac{a^2}{x^2}\frac{1}{e^{-a/x}-1}\right)\left(\frac{-a}{x^2}\right)=\left( \frac{a^3}{x^4}\right)\frac{1}{1-e^{-a/x}} \]

SymPy also can do this calculation

a,x = symbols(' a x')
f = integrate( x**2/(exp(-x)-1 ),(x,0,a/x) )
ans = diff(f,x)
ans