Questions 55 - 58
Contents
Questions 55 - 58#
Q55 Double pendulum#
(a) Assuming that all angles are small during the motion, find the secular determinant for two rigid linked pendulums as shown in the diagram. The pendulums have lengths \(L_1\) and \(L_2\) and masses \(m_1\) and \(m_2\) at their ends. The rods are stiff but weightless and the bearing connecting the upper rod to its mount and that between the rods is frictionless. Because the equations produced are complex, in the last step of the calculation, assume that the pendulums have the same length \(L\).
(b) Use python/Sympy to solve the determinant and show that the normal mode frequencies are given by \(\omega^2 =(1\pm \sqrt{M})g/L\) where \(M=m_2/(m_1 +m_2)\).
(c) Suppose the linkage is a spring with force constant \(k\) whose potential energy varies as \(k(\theta_2)^2/2\); recalculate the oscillation frequencies.
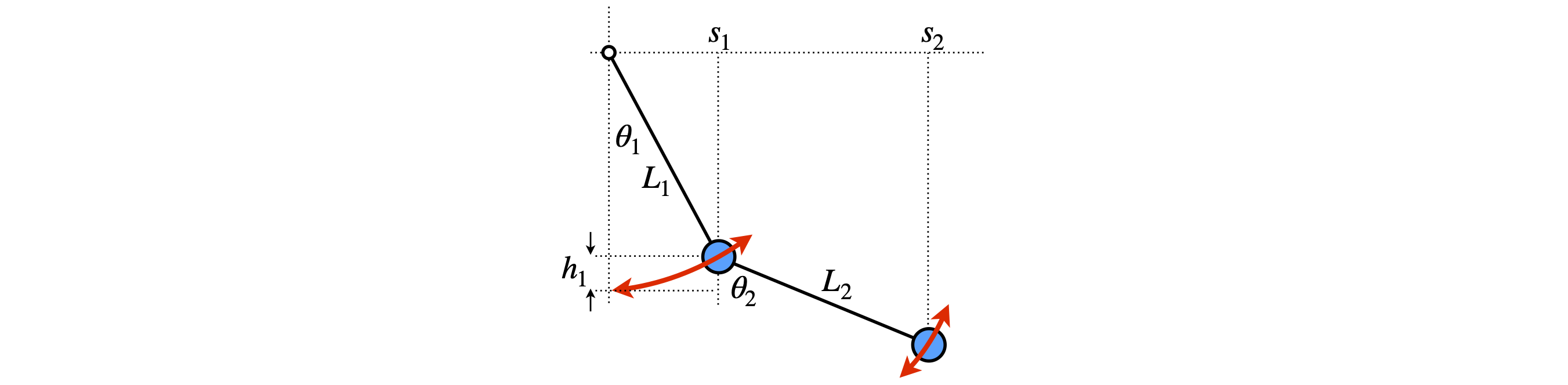
Figure 63. Double linked pendulum. The angles are greatly exaggerated, for in this calculation, only small angle motion is accurately described.
Strategy: Work out the potential energy and differentiate this to find the force. The potential energy against gravity is that due to the vertical height raised from the stationary pendulums. Take them in turn and make \(s_1\) and \(s_2\) the horizontal displacements. The mass needed in working out the potential energy of the upper pendulum is the total mass \(m_1 + m_2\). To see this, assume that the lower pendulum hangs vertically, then, clearly, lifting the upper pendulum involves lifting both masses.
Q56 Masses on springs#
Two similar masses are joined together by three springs fixed at either end to rigid walls, as in the figure, and are free to slide on a frictionless surface. Calculate the normal mode frequencies and sketch their geometry if the force constant of the middle spring is n times that of the outer two. Assume Hooke’s law applies to the springs.
Strategy: Calculate the potential energy by defining displacements of each mass, then work out the force equation as in equation 53.
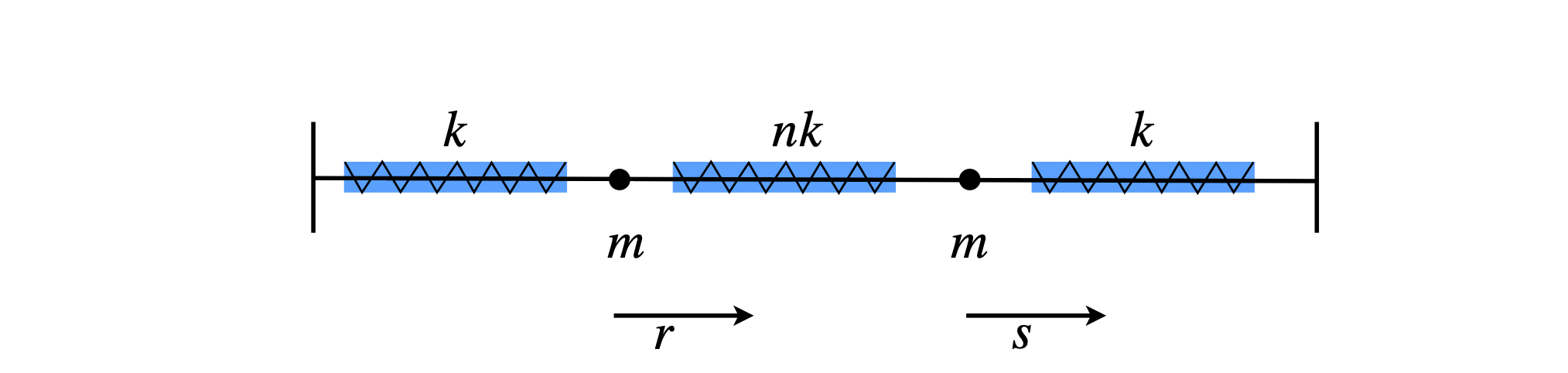
Figure 64. Two masses fixed between three springs. The masses are displaced by \(r\) and \(s\).
Q57 Bending normal mode#
Calculate the bending normal mode for a linear molecule, in a related manner to that used in the example of the stretching modes. Use the displacement vectors shown in the figure, which are in the plane of the figure. Assume that the bending motion obeys Hooke’s law. The force constant is that to bend the molecule rather than to extend its bonds.
(a) Sketch the bending normal modes.
(b) Calculate the normal mode frequencies of the molecule, such as CO\(_2\), by considering the displacement of each atom.
(c) Calculate the correct relative displacements of the atoms.
Strategy: To determine the potential energy, use only force constants for bending between atoms 1 and 2, and between 2 and 3. Once the energy is calculated, the force matrix can be set up and solved. There will be two degenerate bending modes in the molecule, giving \(3N - 5 = 4\) in total. Two have been identified in the example in the text, which leaves two remaining; one of them is bending in the plane of the figure and the other one is perpendicular to this.
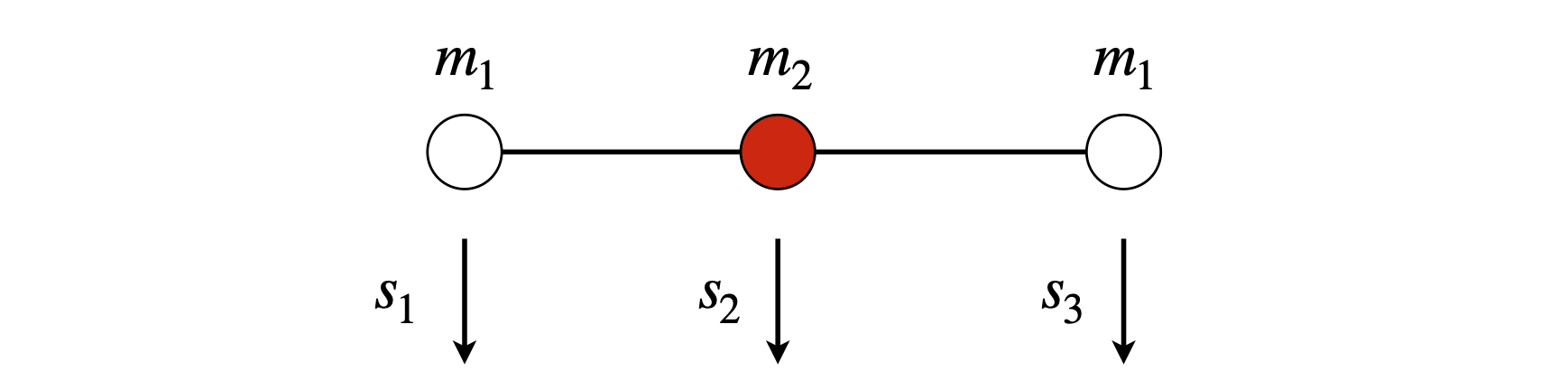
Figure 65. Basis set vectors for a bending mode.
Q58 Vibrations of HC=CH#
Calculate the frequencies and normal mode vibrations of the linear molecule HC=CH, assuming a valence bond potential.
Assume that the force constant for the CH bond is \(1.1\) times that for the CC bond, but that the bending force constants are the same as one another. The experimental vibrational frequencies (degeneracy) are, \(612(2), 619(2), 1974, 3282, 3373 \;\mathrm{cm^{-1}}\).
Decide from your calculation, which are the symmetric and which the asymmetric modes and which the bending modes. Because the algebraic result is very complicated, calculate the eigenvalues and eigenvectors numerically. Use python by modifying Algorithm 7 to this problem.
Strategy: The valence bond potential means that coupling is only to adjacent atoms. As you are asked for all the normal modes, this includes bends as well as stretches. It is advantageous in this case to do the calculation in two parts, because the molecule is linear, and the \(x-, y-,\) and \(z\)-displacements do not depend on one another. The total number of modes is \(3N - 5 = 7\).
Since a numerical answer is required, give the masses their values, (in amu) and use \(k_H = 1.1k_C\). In the eigenvalue (secular) determinant, divide by \(k_H\), as this is a constant to obtain a numerical value, but do not forget then to multiply the resulting eigenvalues by \(k_H\). The eigenvectors are independent of \(k_H\). Use the pattern of these to determine the nature of the normal modes.


