Questions 33 - 38
Contents
Questions 33 - 38#
Q33 Volume of unit cell#
Find the general formula for the volume of a unit cell using equation 30. Simplify the answer as far as possible.
Q34 Bravais lattice#
Determine what Bravais lattices make \(\displaystyle n_2=\frac{\cos(\alpha)-\cos(\beta)\cos(\gamma)}{\sin(\gamma}=0\), see eqn 29.
Q35 Unit cell#
If a space group is monoclinic then \(\alpha = \gamma = 90^\text{o}\) and \(\beta \ne 90^\text{o}\) and the unit cell dimensions are \(a, b, c\). By convention, \(\beta\) is the angle between sides \(a\) and \(c\), see figure 20. Show that the bond distance between two atoms is the same using equation 21 as equation 34.
Q36 Basis set for crystal#
(a) Write down a basis set to define the position of atoms in a tetragonal, orthorhombic or cubic crystal with sides \(a, b, c\), and calculate the angle \(\theta\) if point 4 is \(a/3\) along the side.
(b) For a two-dimensional hexagonal structure such as graphite, as shown in the figure, the unit cell axis are at \(60^\text{o}\). The axes can be defined with unit vectors \(\vec{u}\) and \(\vec{v}\). Calculate the lengths \(1-2, 1-3, 1-4, 1-5\), and angles \(2-1-3, 2-1-4\), and \(2-1-5\).
Strategy: (b) The natural basis set should lie along the sides of the hexagonal unit cell and then this is labelled with vectors \(\vec u\) and \(\vec v\). If the basis set is written as \((u, 0), (0, t)\) then this would be an orthogonal set, but the angle between the vectors is \(60^\text{o}\) not \(90^\text{o}\) so this is cannot be right. It is better to transform the vectors into an orthogonal \(x-y\) set using the transformation matrix described in the text; equation 31. As the structure is two dimensional, then the axis \(c\) is zero and the matrix becomes two dimensional. Taking point 1 to be the origin, point 2 is at \((3a, 3a)\), 3 at \((2a, 4a)\), 4 at \((1a, 4a)\), and 5 at \((4a, 1a)\) in \(\vec u\) and \(\vec v\) unit vectors. This can be seen by counting the number of diamond shapes defined by the \(u-v\) basis set needed to cross the hexagons to a given point.
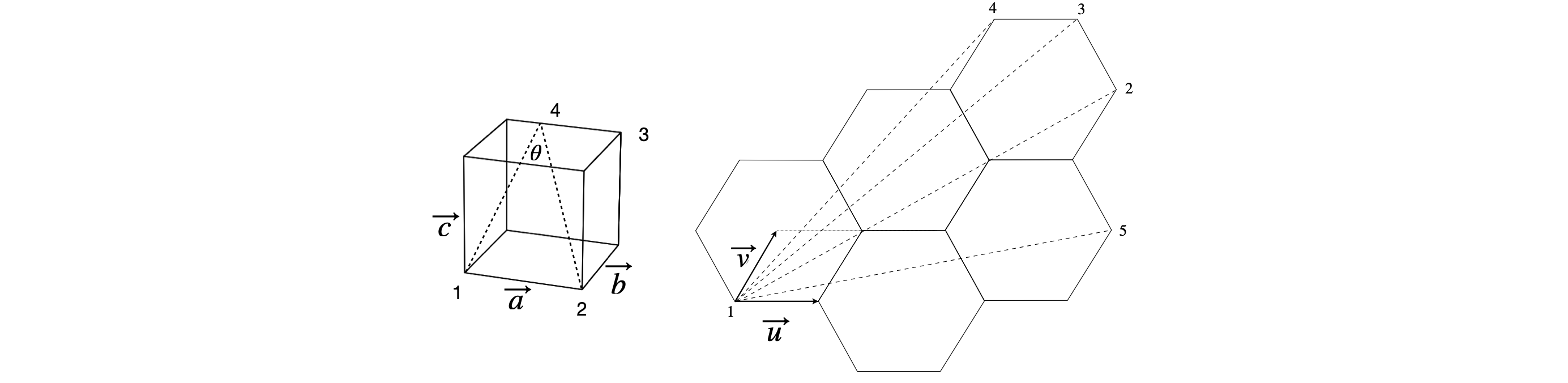
figure 24. Geometry for a cube and hexagonal structure such as graphite.
Q37 Tetrazine bond lengths and angles#
Using Python, repeat the tetrazine example in the text then calculate the \(\mathrm{C-N_2, N_1-N_3}\) bond lengths and \(\mathrm{CN_1N_3}\) bond angle.