Questions 59 - 62

Q59 XeF\(_4\) moments of inertia.

Calculate the moments of inertia of the planar molecule XeF\(_4\)

(a) about the C\(_4\) symmetry axis and

(b) about a diagonal and also about an edge.

Assume each bond length is \(2 \unicode{x212B}\) .

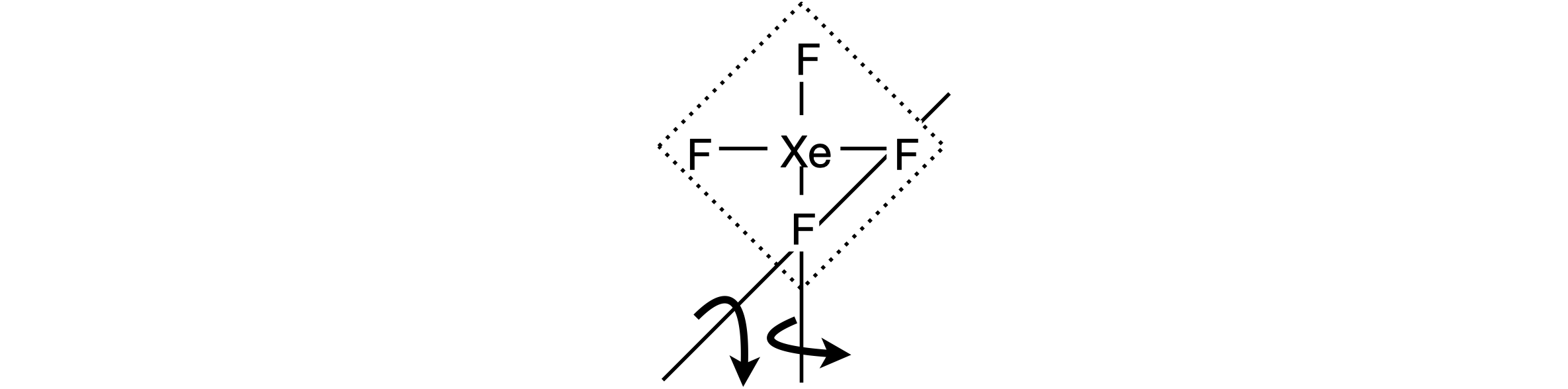
Figure 67 XeF\(_4\) and two rotation axes.

---

Q60 Loop of wire

A circular loop of wire is formed by n rigidly connected masses with radius \(R\) of total mass \(M\). Explain the different values obtained for the moment of inertia,

(a) About an axis z, through the centre of the loop,

(b) about a diameter,

(c) About an edge and parallel to \(z\).

The difference in moments of inertia, is illustrated in Figure 68, and in the right-hand diagram where the loop rotates about an edge.

Strategy: For a planar body to simplify the calculation, use the perpendicular axes theorem \(I_z = I_x + I_y\) and by symmetry \(I_x = I_y\).

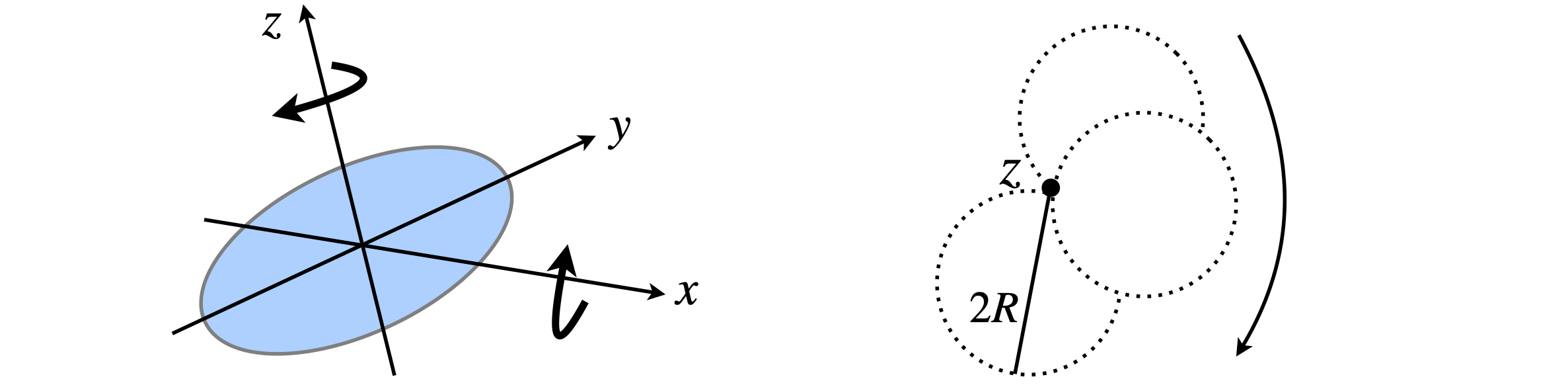
Figure 68 Rotation of a loop about different axes.